OpenAI假设被推翻!给定计算量,较小模型打败大模型,Llama 2训练与GPU计算关联度
2023-08-02 07:37:15 来源: 新智元
模型推断时,避免将算力浪费在缓慢收敛上至关重要。
 (资料图片)
(资料图片)
孙子兵法的一句话「多算胜,少算不胜」,便阐尽了这个道理。
Chinchilla究竟是什么?较小的模型,乘法少,因此它们跑得更快,训练得也快。
然而,通常人们认为,小模型最终会达到知识能力的极限,学习速度会变慢。
而一个具有更大规模的模型,将超过小模型,并在给定的训练时间内取得更好的性能。
在评估模型如何在训练期间获得最佳性能时,OpenAI和DeepMind都试图绘制帕累托边界(Pareto frontier),但他们没有明确说明是使用该理论绘制的。
不过,OpenAI最近的一句话暗示着这一假设:
我们期望较大的模型总是比较小的模型表现更好。[…] 大小固定的模型将受到GPU容量限制。
这一假设是OpenAI计算帕累托边界的基础。
在此,我们先介绍下DeepMind成员在2022年的工作Chinchilla模型,其技术原理和其他同类模型一样(比如GPT-3) ,区别在于训练参数和数据量。
DeepMind宣称,「对于计算优化训练,模型大小和训练数据集大小应该相等地缩放: 模型大小每增加一倍,训练数据集大小也应该加倍。」
图片
Chinchilla AI通过使用与Gopher相同的计算预算,但具有70B个参数和4倍多的数据,来训练一个计算更优化的模型Chinchilla ,从而来检验这一假设。
验证结果表明Chinchilla 在大量下游评估任务中明显优于 Gopher、GPT-3、Jurassic-1 和 Megatron-Turing NLG。
Chinchilla 在MMLU 基准测试中的平均准确率达到 67.5%,比 Gopher 提高了 7% 以上。
图片
在Chinchilla的工作中,如图显示了不同大小模型大量训练运行的训练损失。
乍一看,这些曲线遵循理论:较小的模型最初损失较低,但最终速度变慢,并被较大模型的曲线超越。
图片
在图表中,较小的模型性能低于较大的模型时,都标记成灰点。灰色线,即帕累托边界,是计算比例定律的方式。
这个假设的问题在于,我们不知道如果让较小的模型训练更长时间会发生什么,因为一旦它被超越,他们就停止训练。
让我们来看LLaMA。
Chinchilla能复刻Llama曲线吗?今年早些时候,Meta训练了4个不同大小的模型。与其他模型不同,研究人员对每一个模型都进行了大量的训练,即使是规模较小的模型。
他们还发布了训练运行曲线:
图片
1. 每条曲线首先在幂定律中直线下降
2. 然后似乎进入了一个近乎线性的损失递减过程(与相当恒定的知识获取率相对应)
3. 在曲线的最末端,它们都变得稍微平缓
首先,我们想谈谈人们对「曲线末端变平坦」的一个微妙误解。
它们都是通过使用可变学习率的梯度下降法进行训练的(学习率大致是一个超参数,用于确定向梯度方向移动的幅度)。
为了获得良好的训练效果,它们必须不断降低学习率,这样才能在源素材中检测到更微小的模式。
而它们使用的降速公式是最广泛使用的:余弦时间表(the cosine schedule)。
图片
正如从图表中看到的,在训练快结束时,余弦时间表停止以产生良好的、近线性的训练损失曲线的速度降低学习率。
学习速度的减慢就是这样导致的结果。模型还是可能有能力以同样接近线性的速度来学习。
事实上,如果我们给它更多的文本,就会拉长余弦时间表,这样它的学习率就会以同样的速度继续下降。
模型的适应情况并不依赖于,我们可以为其训练提供的数据量。因此,学习率下降的变化是不合理的。
不过,这不是本文的重点。
训练损失曲线可能会以另一种方式误导我们。
当然,它们都是在相同的数据上训练的,但它们不会以相同的速度处理这些数据。
我们想知道的不是模型的样本效率又如何(在这方面,较大的模型显然从它所看到的数据中学到更多东西)。
让我们想象一场比赛:所有这些模型都在同一时间开始,我们想知道哪一个先越过终点线。
换句话说,当在训练中投入固定计算量时,谁在这段时间里学得最多?
值得庆幸的是,我们可以将损失曲线与Meta提供的另一项数据结合起来:每个模型训练所花费的时间。
图片
图片
首先要说明的是,我们看到的整个Chinchilla图形只覆盖了这个图形左边的一小块。
在这一小片区域中,我们看到了与Chinchilla记录相同的行为。
以7B为例:一开始,它的损耗下降速度比更大的模型快得多,然后速度减慢,13B模型超过了它,首先达到了1.9。
但是,接下来是一个遥远的、意想不到的转折:
7B进入一个近乎线性的状态,呈陡峭的下降趋势,似乎正在再次超越13B?很难从这张图上看出如果7B训练得更久会发生什么。
然而,13B和33B之间似乎也有同样的行为,最初的Chinchilla减速也近乎线性的状态,此时13B下降得很快。
就33B来说,它的计算时间是13B两倍,因此超越13B理所当然。
33B和65B之间也出现了同样的先减速后加速的情况,以至于33B实际上从未被65B超越。
图表显示的情况打破了OpenAI和Chinchilla的假设:更大的模型还没有赢(尚未)。他们检测到的速度减慢实际上并不是因为达到了某个容量极限!
不过,7B曲线还是有点不尽人意。如果Meta对其进行更长时间的训练就好了... 而现在,他们做到了!Meta本周发布了 LLaMA 2!
证实「质疑」图片
同样,Llama 2也公布了模型的训练时间:
图片
图片
一眼望去,我们就会发现训练曲线与LLaMA 1并不一致,即使模型完全相同。
原来,LLaMA 2是在双倍的上下文大小和更长的余弦时间上进行训练的,不幸的是,这对所有大小的模型都产生了负面影响。
不过,较小模型受到的影响比较大模型更严重。
因此,在 LLaMA 1中,34B模型在任何训练时间内都始终优于65B模型,而现在则略高于70B模型,之后又超过了70B模型:
图片
更重要的是,对训练速度的比较有力地证实了我们对LLaMA 1的猜测:
1. 首先,它们比更大的模型更快,
2. 然后,它们放慢速度,被较大的模型超越(根据Chinchilla的说法)
3. 但随后,它们又进入了近似线性的状态,在这种状态下,较小的模型会以更陡峭的速度下降,从而获得更优越的知识,并再次超越较大的模型!
一个有趣的结果与开始训练时做出正确的选择有关:与人们普遍认为的相反,更大的模型会产生更差的结果。
如果必须选择参数大小和数据集,最好选择一个7B模型,并在数万亿个token上训练7个epoch。
看看7B的近线性机制,再推断一下70B模型的停止时间:如果把70B的计算用在7B模型上,那么它可能会达到更低的困惑度(perplexity)!
我们从LLaMA 2中注意到的另一件事是,LLaMA 1曲线末端的学习速度减慢确实是余弦时间表的一个假象。
在LLaMA 2的训练中,读取1万亿token的相应时间点上完全没有出现这种放缓现象。
事实上,在同样token下,LLaMA 2 7B模型比LLaMA 17B模型质量差,原因可能是它的余弦时间表被拉长了!
让我们回到Chinchilla的论文来论证这一点。在附录A图A1 中,他们展示了针对各种余弦时间表参数的消融研究(拉伸学习率曲线的各种方法)。
图片
他们指出,当曲线不被拉长时,损失最低。图表证明了这一点,但作者也注意到了一些不对劲的地方。
在读取了600万个token后,顶部模型的训练损失低于2.8。与此同时,在同一标记处,底部模型的训练损失高于2.8。
然而,模型之间唯一的区别就是余弦时间表!
由于底层模型需要训练更多的数据,因此「未拉伸」余弦值被计算为更多的步骤,这有效地拉伸了它。
如果学习率遵循分配给更少训练步骤的时间表,那么在相同的训练时间内会有更好的损失。
更广义地说,这就提出了一个问题:如果余弦时间表不是最优的,那么曲线的尾部形状应该是怎样的呢?
参考资料:https://espadrine.github.io/blog/posts/chinchilla-s-death.html#Can_Chinchillas_picture_a_Llama_s_sights
热点推荐
-

工龄与退休后工资领取对照表 工龄30年能领多少退休金?
-
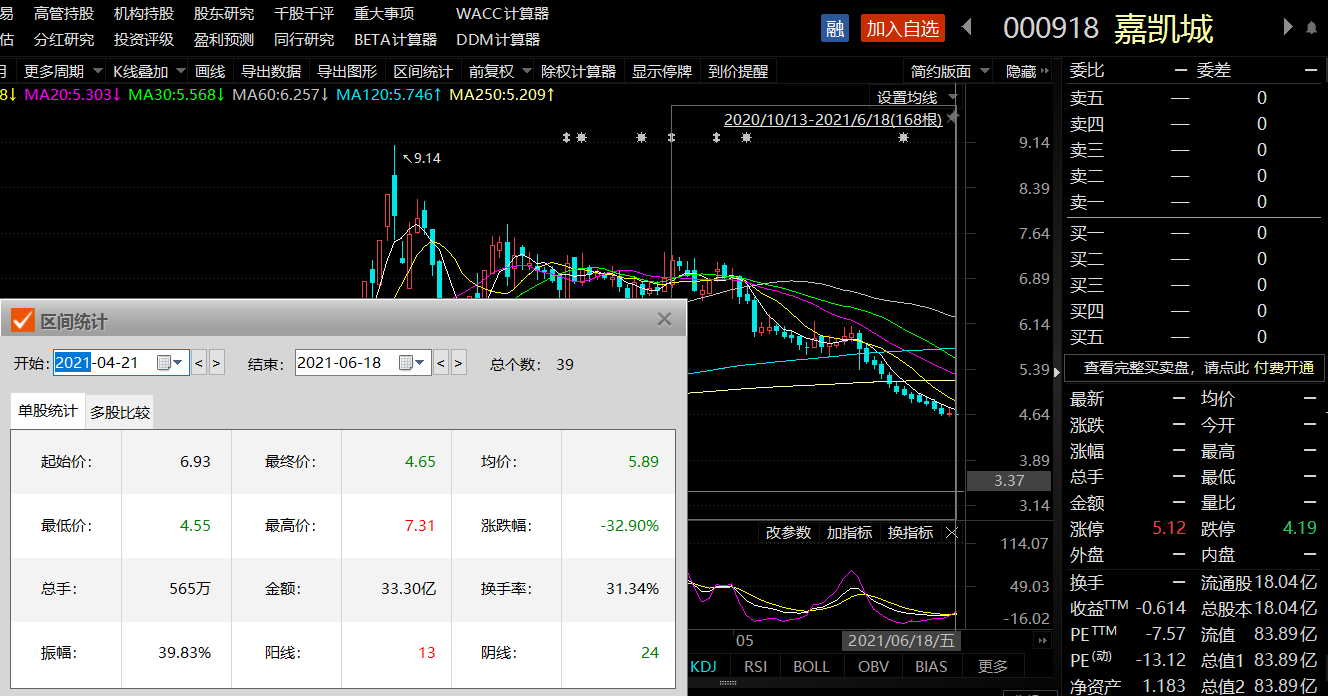
嘉凯城(000918.SZ)今日起临时停牌 复牌时间未知
-
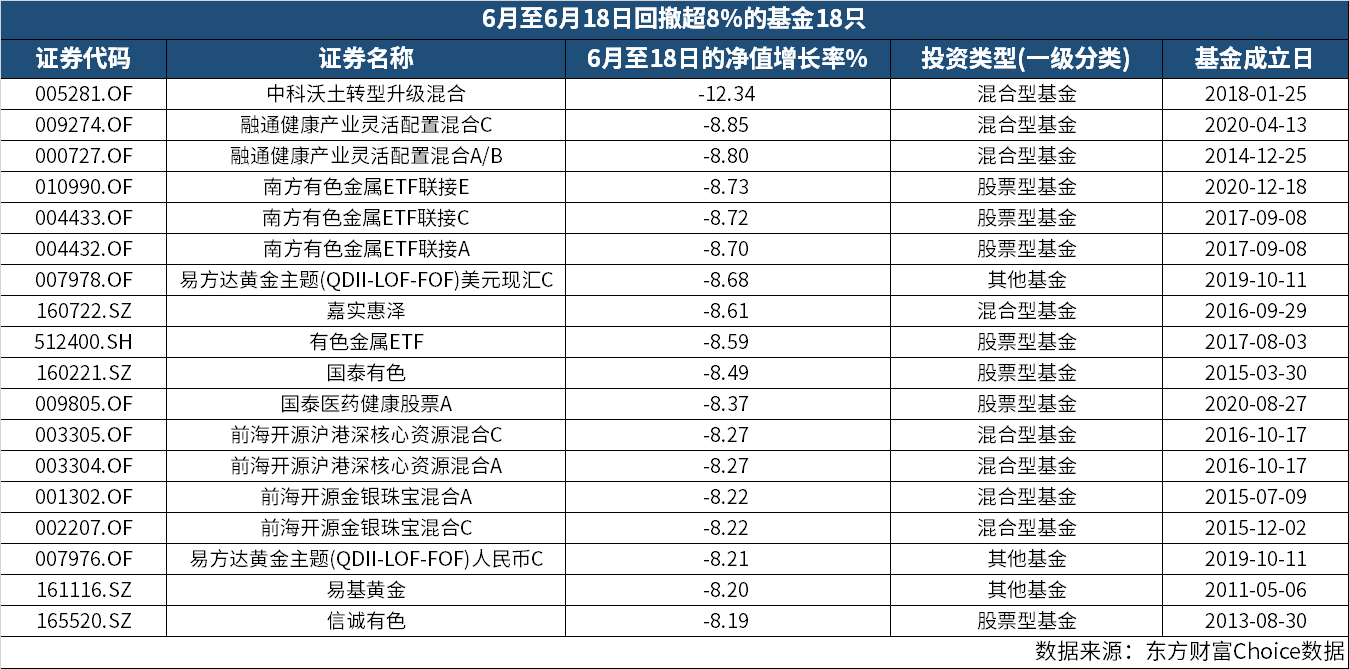
中科沃土转型升级混合 6月回撤已超12%
-
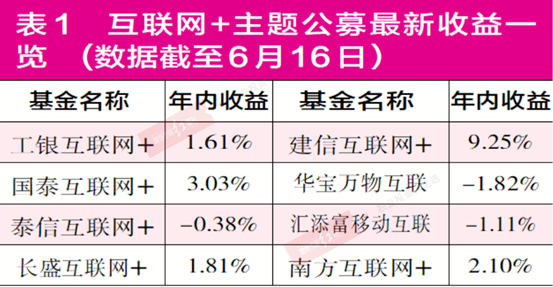
“互联网+”产品普遍举步维艰 多家产品被“深套”
-
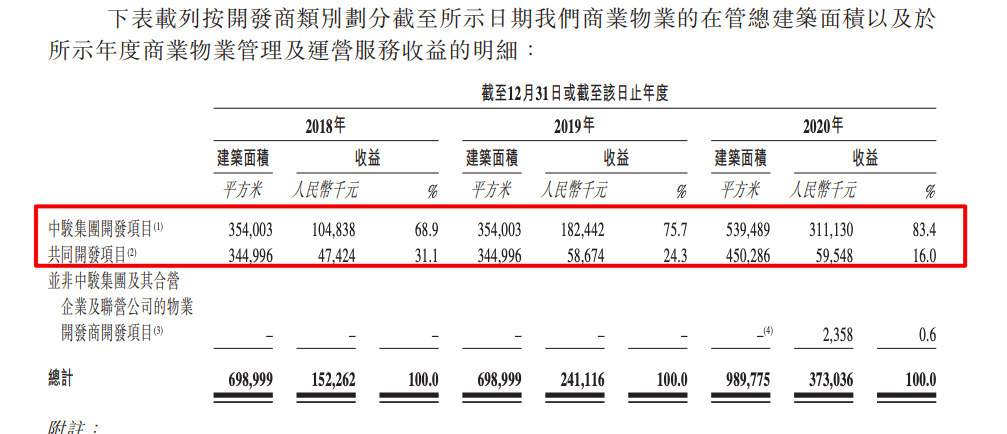
中骏商管将挂牌 中骏控股集团持股62.43%
-

OpenAI假设被推翻!给定计算量,较小模型打败大模型,Llama 2训练与GPU计算关联度
-

两部门紧急预拨1.1亿元资金 支持京津冀地区做好防汛救灾工作
-

令人惊艳的不只是设计,领克08还藏了哪些惊喜?
-

反担保的含义及目的有哪些
-

【短讯】直播电商概念复苏逆市走强 超导概念突然爆发|港股风向标
-

俄联合航空制造集团:计划2026年前生产18架MS-21飞机和超40架SSJ-NEW客机
-

不敢想象,23岁小将出任湖人首发,詹姆斯浓眉力挺
-

“旅游+”焕发连云港“大花果山”暑期文旅消费新活力
-

王者荣耀:你的吕布,第一件装备还在出苍穹?逐风才是最佳选择
-

江洲湾项目,提质加力!
-

广弘控股:公司广弘农牧兴宁项目目前正在加快建设工作,预计今年将建成投产
-

赛力斯发布7月产销快报 AITO问界M9将搭载HarmonyOS 4
-

中国队获成都大运会乒乓球男子团体冠军
-

10省份上半年经济增速低于一季度 哪些因素拖累了增长?
-

新英雄海诺即将上线体验服 技能曝光:双形态,有远、近距离两种攻击方式
-

今世缘(603369.SH):公司的业绩是基本符合预期的
-

█ 干了20年采购,我越发简单了 █
-

泉州夯实基础设施建设推动数字经济发展
-

联想y480配置怎么样 联想y480配置介绍 联想y480咋样啊
-

港股异动|重庆钢铁股份(01053)A股涨停 H股飙涨逾17% 业内预期下半年钢企盈利转强
-

头球之王!C罗超越盖德穆勒成打入头球最多的球员
-

(成都大运会)下水数百次 他的大运会在角落也在心中
-

“藏蓝”邂逅“迷彩” 浙江武警官兵传承三代人梦想
-

广西北海市市场监管部门开展暑期校外培训机构、托管班专项检查
-

越南电动汽车制造商VinFast计划8月在美国上市